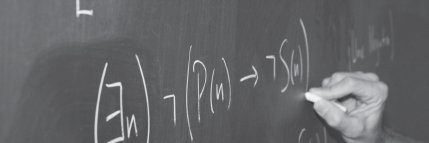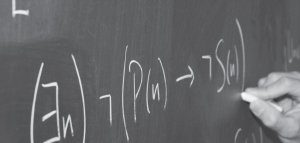Get lifelong access to this course for only $4.95 (US)!
In Level 2: Properties & Relations we learned to construct truth-tables and how to use these logical devices to determine the logical properties of individual statements and logical relationships between statements. And in Level 2: Proof By Analogy we were introduced to the concept of validity and how to use the form of an argument to test its validity. In this course we will bring these two topics together and learn how to use truth-tables to test any argument – no matter how unfamiliar its form – for validity.
Consider the following affirming the consequent argument:
| (P | → | Q) |
| Q | ||
| P |
Now, let’s set this argument out horizontally as a truth-table:
| (P | → | Q) | Q | ⊧ | P | ||
| T | T | T | T | T | 1 | ||
| T | F | F | F | T | 2 | ||
| F | T | T | T | F | 3 | ||
| F | T | F | F | F | 4 |
As we can see, there is one line (line 3) upon which the two premises of the argument are both true, but the conclusion of the argument is false. As there is a “TTF line” in the truth-table, it must be possible for the premises to be true and the conclusion false at the same time. Thus, we can see from the truth-table that the argument is invalid.
But how do things look when we are dealing with a valid argument? Consider the following modus ponens argument:
| (P | → | Q) |
| P | ||
| Q |
Now, let’s set this argument out horizontally as a truth-table:
| (P | → | Q) | P | ⊧ | Q | ||
| T | T | T | T | T | 1 | ||
| T | F | F | T | F | 2 | ||
| F | T | T | F | T | 3 | ||
| F | T | F | F | F | 4 |
As we can see, there is no line on this truth-table upon which both premises are true and the conclusion is false. The only line upon which both premises are true is line 1, and on line 1 the conclusion is also true.
This course contains 3 Lessons, each of which contains a number of videos explaining key concepts and a number of electronic quizzes for you to apply an solidify your understanding of the concepts contained in the course.
Lesson 1: Proofs of Commons Forms AVAILABLE AS FREE SAMPLE LESSON!
Lesson 2: Complex Versions of Common Forms
Lesson 3: Uncommon Forms