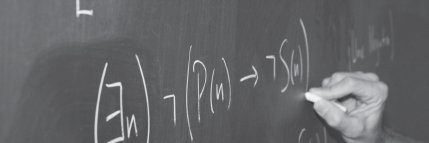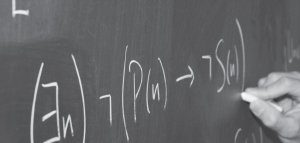Get lifelong access to this course for only $4.95 (US)!
Truth-tables are powerful tools with a variety of applications in logical analysis. In the first part of this course you will learn to construct truth-tables for logical formulae. Next, you will learn to use these truth-tables to identify the logical properties of statements. Here’s an example:
“It is currently raining in Paris or it is not currently raining in Paris.”
Intuitively, we know that this sentence must be true, and we can prove this using a truth-table. The first step is to analyse the sentence. Here’s what the entire analyzed sentence looks like with the truth-values filled out under the simple sentences:
P = “It is raining in Paris”
| (P | ∨ | ~ | P) |
| T | T | ||
| F | F |
And, here’s how it looks when we fill out the entire truth-table:
| (P | ∨ | ~ | P) |
| T | T | F | T |
| F | T | T | F |
Now, focus on the truth-values under the operator with the broadest scope, “∨”. The truth-value under the broadest operator on a given row is the truth-value of the entire formula on that row. And as we can see, the truth-value under the main operator “∨” is T on both rows. This means that (P∨~P) is always true, no matter what the truth-value P happens to be. Thus, (P∨~P) is a necessary truth.
Let’s look at another example:
“It is currently raining in Paris AND it is not currently raining in Paris.”
Intuitively, we know that this sentence must be false, and we can prove that this using a truth-table. Again, the first step is to analyze the sentence. Here’s what the entire formula looks like with the truth-values filled out under the simple sentences:
P = “It is raining in Paris”
| (P | & | ~ | P) |
| T | T | ||
| F | F |
And, here’s how it looks when we fill out the entire truth-table:
| (P | & | ~ | P) |
| T | F | F | T |
| F | F | T | F |
Now, focus again on the truth-values under the operator with the broadest scope, which this time around is “&”. The truth-value under the broadest operator on a given row is the truth-value of the entire formula on that row, and as we can see, the truth-value under the main operator “∨” is F on both rows. This means that (P&~P) is a necessary falsehood. It is false no matter what the truth-value of P.
Once we have mastered the use of truth-tables for identifying logical properties, we will learn to use truth-tables to test for relations of consistency, contradiction, equivalence and entailment within pairs of formulae. In Level 4: Using Truth-Tables To Test For Validity, we will once again return to the topic of truth-tables, this time using them to test argument forms or sequents for validity.
Here is a complete list of lessons for this course:
Lesson 1: Mastering the Logical Operators AVAILABLE AS A FREE SAMPLE LESSON!
Lesson 2: Truth-Tables for Logical Formulae
Lesson 3: Logical Properties
Lesson 4: Equivalence
Lesson 5: Contradiction & Consistency
Lesson 6: Entailment
Lesson 7: All Four Relations